十字相乘法——因式分解是提高分解速度的最佳方法

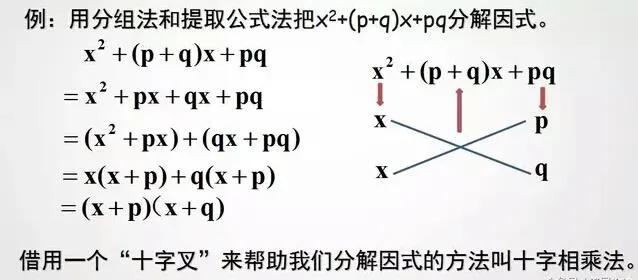
十字相乘法是一种高效的因式分解技巧，尤其适用于一元二次多项式的分解。这种方法的核心在于将复杂的因式分解过程简化为直观的十字交叉运算，从而快速找到多项式的因式。

十字相乘法的基本原理是利用二项式乘法的逆运算。具体来说，对于一个形如ax²+bx+c的二次三项式，我们可以将其分解为(a1x+c1)(a2x+c2)的形式。其中，a1和a2的乘积等于a，c1和c2的乘积等于c，而a1c2+a2c1则等于b。通过十字交叉的方式，我们可以直观地表示这一过程：左上角的a1与右下角的c2相乘，右上角的c1与左下角的a2相乘，然后将这两个乘积相加，得到的结果应该等于b。

这种方法的优势在于它提供了一种系统化、可视化的解题思路。相比传统的试错法，十字相乘法能够更快地找到正确的因式组合。例如，对于多项式6y²+19y+15，我们可以通过十字相乘法快速分解为(2y+3)(3y+5)。这种方法不仅节省时间，还能减少计算错误的可能性。

然而，十字相乘法并非万能的。它主要适用于二次项系数和常数项可以轻松分解为整数因数的情况。对于一些复杂的多项式，特别是那些系数较大或为分数的情况，十字相乘法可能就显得力不从心了。此外，对于高于二次的多项式，这种方法也难以直接应用。

尽管如此，十字相乘法仍然是数学教学中一个非常有价值的工具。它不仅能够帮助学生快速掌握因式分解的技巧，还能培养他们的逻辑思维能力和模式识别能力。通过反复练习，学生可以逐渐掌握这种方法的精髓，并将其应用到更广泛的数学问题中。

总的来说，十字相乘法是一种简单而强大的数学技巧，它为因式分解提供了一个直观、高效的解决方案。虽然它并非适用于所有情况，但在处理一元二次多项式时，这种方法无疑是一个提高解题速度和准确性的有力工具。