对实数我们知道多少？

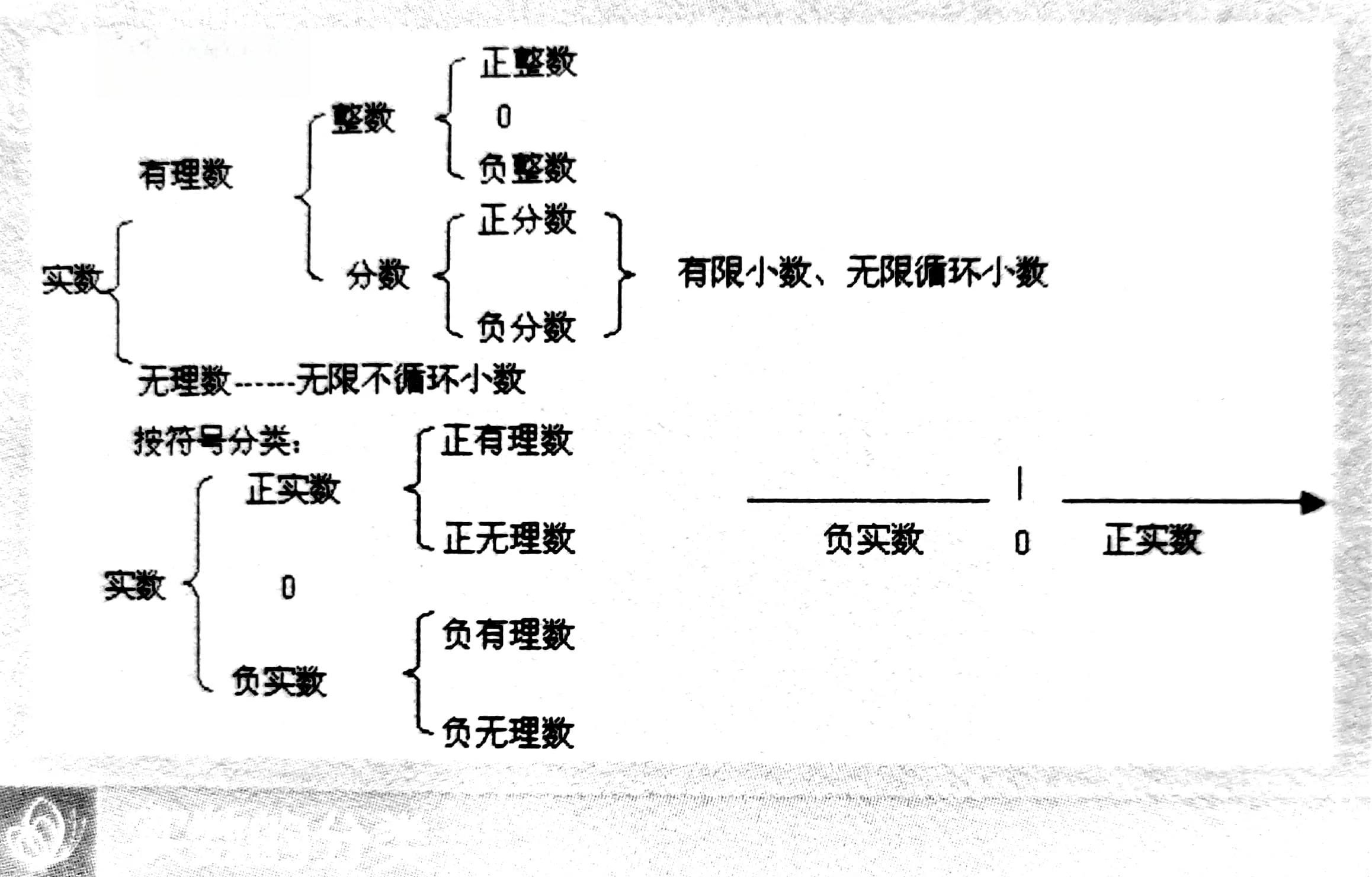
实数，这个看似简单的数学概念，实际上蕴含着人类对数的认识从具体到抽象、从有限到无限的漫长历程。从古希腊数学家的困惑，到19世纪数学家的严格定义，实数的概念经历了数千年的演变和完善。

实数的概念最早可以追溯到古希腊时期。公元前500年左右，以毕达哥拉斯为首的数学家们已经认识到有理数在几何上存在局限性。例如，边长为1的正方形对角线长度无法用有理数精确表示，这直接挑战了毕达哥拉斯学派“万物皆数”的信念。这一发现引发了著名的“第一次数学危机”，促使数学家们开始思考更广泛的数的概念。

然而，实数的概念真正被广泛接受是在17世纪。随着微积分学的兴起，实数作为连续变化量的数学模型，其重要性日益凸显。到了19世纪，数学家们开始对实数进行严格的定义。1871年，德国数学家康托尔首次提出了实数的严格定义，标志着实数理论的正式确立。

实数的引入极大地推动了数学的发展。它不仅为微积分提供了坚实的理论基础，还为数学分析、拓扑学等现代数学分支的建立铺平了道路。实数的完备性（即戴德金完备性）是微积分理论的核心，保证了极限、连续性等概念的合理性。

在现代数学中，实数集通常用黑体字母R表示。它是一个完备的有序域，具有许多重要的性质。例如，实数集是不可数的，这意味着实数的个数远多于自然数。实数集还具有稠密性、阿基米德性质等重要特征，这些性质使得实数成为描述连续变化的理想工具。

实数不仅在纯数学中扮演着重要角色，在物理学、工程学等领域也有广泛应用。从测量长度到描述物理定律，实数都是不可或缺的数学工具。在计算机科学中，尽管计算机只能存储有限精度的实数（通常用浮点数表示），但实数的概念仍然是理解和设计数值计算算法的基础。

总的来说，实数的发展历程反映了人类对数学本质的不断探索。从最初的困惑到严格的定义，实数的概念不断完善，最终成为现代数学的基石之一。它不仅解决了古希腊数学家留下的难题，还为数学和科学的发展开辟了新的道路。实数的故事告诉我们，数学的进步往往源于对基本概念的深入思考和不断探索。