用了很多年的平方等于重力加速度g，这句话到底对不对？

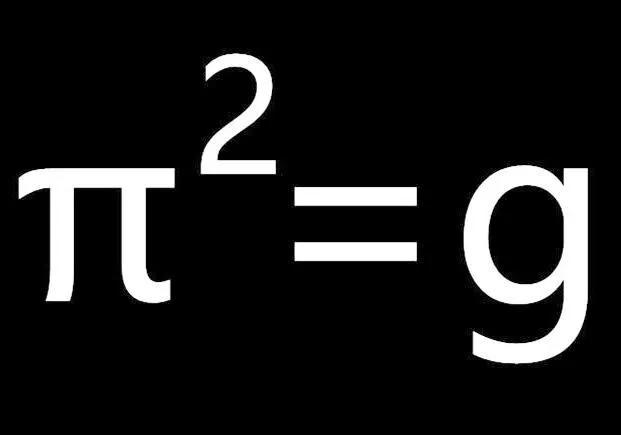
“π平方等于重力加速度g”这个说法在中学物理教学中广为流传，许多人将其视为一个正确的等式。然而，这个看似简单的等式背后，却蕴含着深刻的科学原理和历史背景。

圆周率π是一个数学常数，表示圆的周长与其直径的比值，约等于3.14159。它是一个无理数，即无限不循环小数，在数学和物理学中有着广泛的应用。相比之下，重力加速度g是一个物理量，表示物体在重力作用下自由下落时的加速度，通常取值为9.8米/秒²。

这个等式之所以流传，源于一个历史上的巧合。1790年，法国国民议会曾将“米”定义为纬度45度海平面上半周期为1秒的单摆的摆长。在这个定义下，可以计算出g约等于π²。然而，这个定义很快就被废弃了，因为科学家们意识到单摆的定义还涉及到时间，以及秒这个单位。

事实上，重力加速度g的计算公式是g = GM/r²，其中G是引力常量，M是地球质量，r是物体与地球中心的距离。这个公式清楚地表明，重力加速度不仅与地球质量有关，还与物体的位置密切相关。随着高度的增加，重力加速度会逐渐减小。在地球表面，重力加速度的值介于9.78 m/s²和9.83 m/s²之间，具体数值取决于纬度等因素。

此外，地球的自转也会对重力加速度产生影响。在赤道上，由于离心力的作用，重力加速度会稍微减小。因此，即使在同一高度，不同纬度的重力加速度也会有所不同。

尽管“π平方等于重力加速度g”这个等式在某些特定条件下看似成立，但它本质上只是一个近似值。在实际应用中，我们不能简单地将这个等式当作普遍适用的公式。在进行精确计算时，我们需要考虑物体的具体位置和高度，使用更准确的重力加速度值。

总的来说，圆周率π是一个永恒不变的数学常数，而重力加速度g则是一个随位置变化的物理量。这两个看似相似的数值，实际上代表了完全不同的概念。因此，“π平方等于重力加速度g”这个说法虽然在某些情况下看似成立，但它并不能反映这两个量的本质差异。在科学研究和工程应用中，我们应当谨慎使用这个等式，确保计算的准确性和可靠性。